It’s annual planning time for many companies, with discussion and debate about where to make investments. A key aspect of product management is the creation of financial models predicting future outcomes in order to make informed investment decisions. “If we spend x dollars to build the product and can get n users to pay us y dollars each year, we’ll bring in revenue of z dollars”. But the approach and tools we use are often simplistic and do a poor job of accounting for real-world uncertainty. Monte Carlo simulation is a tool that allows us to improve our predictions when dealing with uncertainty. Named for the Monte Carlo Casino in Monaco, it works by calculating and averaging out thousands of possible outcomes across a range of given inputs. In this post we’ll explore the why and what of Monte Carlo simulations, and in a future post we’ll walk through how to create our own Monte Carlo simulation.
Why build a model at all?
The purpose of a financial model or business case is to predict some future financial outcome that is the result of the interactions of a set of known or assumed inputs, in order to make an investment decision.
Let’s assume we’re evaluating whether to move forward with a hypothetical online subscription service which will:
- cost some money to build
- have some per-user annual run cost
- earn some subscription fee per user per year
- have some level of user adoption, which will grow over time
We’ve kept the example simple so we can focus on the dynamics; in practice your model is likely to be more complicated, with other cost components and adoption elements that you’ll want to factor in.
First-cut: a simplistic approach
Here’s a simple version of our model, with the input assumptions on the left feeding into some prediction of future revenues and net income over a four-year period. Development is a one-time cost in Year 0. Revenue in a given year is (Annual subscription fee per user X Number of users), while run cost in a given year is (Annual cost per user X Number of users). Each year the number of users grows by the Annual user growth factor (10% in this case).
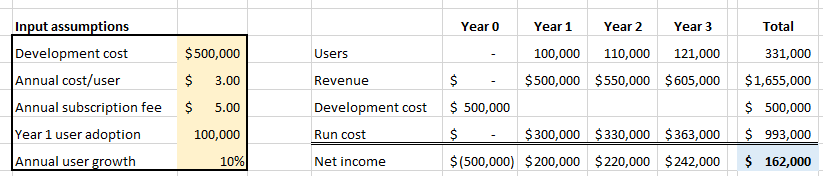
While this approach is fine for simple models with a few well-understood inputs, I’ve also seen it used to make big, multi-million dollar decisions rife with uncertainty!
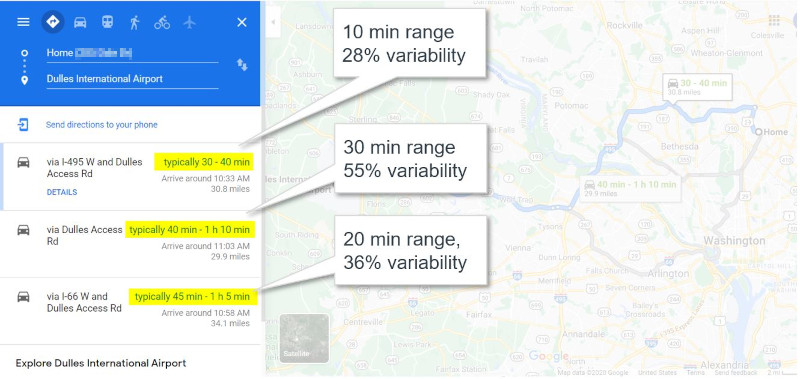
“Google, how long does it take to get to the airport on a Thursday morning?”
Realistic predictions about the future contain variability. We recognize and deal with this in our day-to-day lives. If I’m catching a flight next week, I know there’s a range of time it will take me to get to the airport, and I plan accordingly.
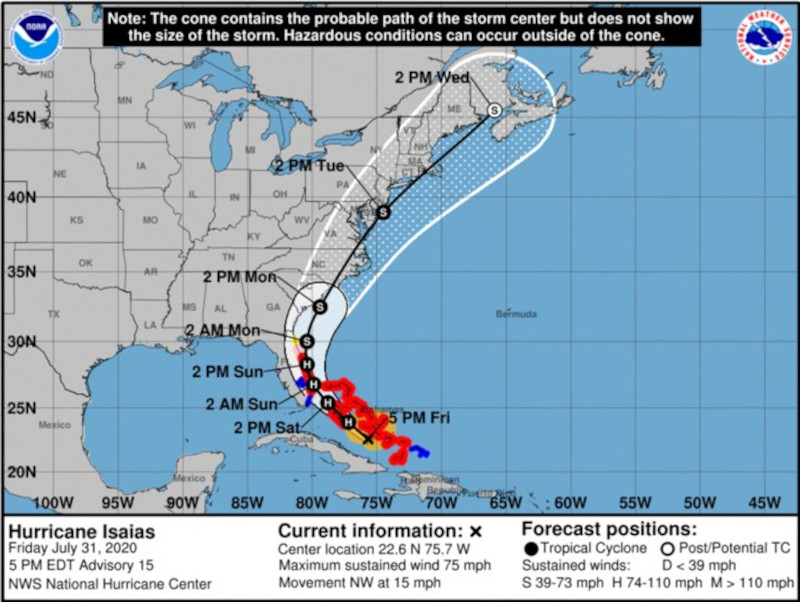
We see this type of variability in all types of predictions. Hurricanes have a “most likely” path. But there’s also a cone of travel that a hurricane could take. And that variability increases the farther out you try to predict.
Take two: a scenario-based approach
So if we’re familiar with uncertainty in these other arenas, why use the simplistic models for our product investment decisions? Not because we don’t recognize that there is uncertainty. I’ve heard and participated in numerous debates about what’s the “right” number to use. “Will our development cost really be $500k, or is it more likely to be $800k? ” “Will we really get 100k users in year one or should we be cautious and use 75k? ” No, we recognize intuitively that there is variability in our inputs. In fact you’ve probably experienced that people are more comfortable giving you estimates in a range. The problem is that it’s hard to conceptualize and model how the interactions of variability among multiple inputs will impact the output.
One attempt to account for uncertainty into our product modeling is to take a scenario-based approach. You’re probably familiar with this. We create three views to model out “optimistic”, “conservative” and “middle-ground” outcomes. This is an improvement, because it puts some bounds on our best-case and worst-case outcomes. In our hypothetical subscription service, that might look like this:
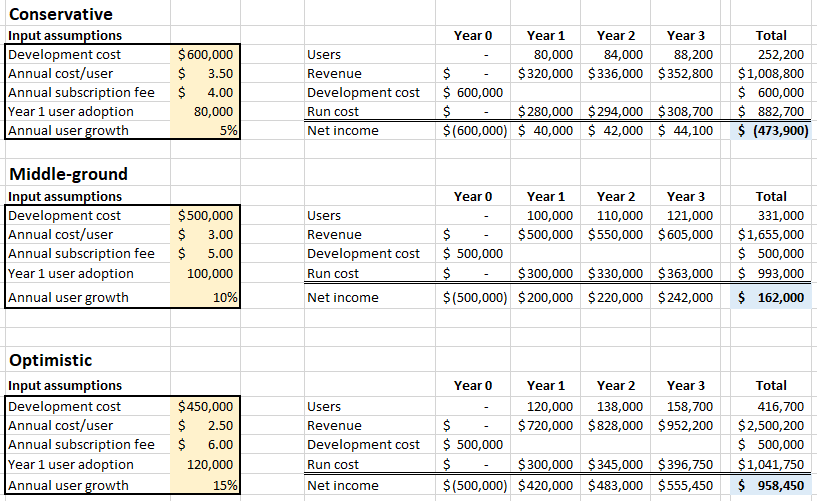
The problem with this approach is that it tends to assume best- or worst- case outcomes for each individual input, with a compounded impact on the outcome. In practice, what are the chances that you hit bad traffic, puncture a tire and have trouble finding parking all on the same drive to the airport?
Monte Carlo to the rescue
The better approach is to use Monte Carlo simulations. This is an approach that allows you to specify uncertainty in your inputs, and propagates those uncertainties into uncertainties in results.
In brief:
- We represent input uncertainties as probabilities (or probability distributions).
- The entire system is simulated a very large (e.g. 1000+) number of times.
- With each simulation, each variable input takes on a value whose likelihood is determined by its probability distribution.
- This results in a large number of separate and independent results, each representing a possible future outcome for the model.
- These independent results are then amalgamated into a probability distribution of outcomes.
In our first simplistic approach we said our four-year net income would be $162k. In our scenario-based approach we said it would likely be $162k, but could be negative $474k or as high as a $958k profit. With a Monte Carlo simulation our predicted net income is going to be a probability distribution like this:
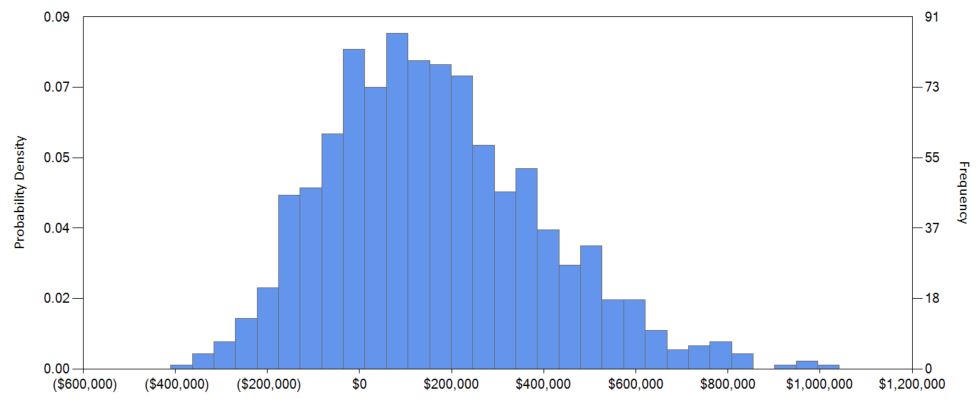
While a little harder to grasp than a single number like $162k, it’s more realistic as a forecast of the future, and allows us to see the range of possibilities we might expect, and the likelihood of those possibilities. Unlike the scenario-based approach it highlights that while those best- and worst-case scenarios are possible, they are far less likely. Importantly, it allows us to translate the individual independent probabilities of our inputs into the combined probability of our range out outcomes.
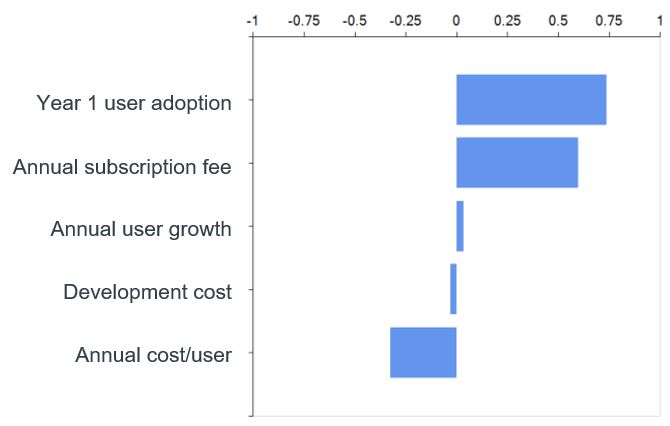
You can also see which of your inputs your model is most sensitive to. This has value because it tells you where your greatest risk might lie, allowing you to focus efforts on mitigating that risk. For example, although development cost is our biggest single input cost and might vary by tens of thousands of dollars, it turns out that our model is much more sensitive to variations of a few cents in our subscription fee, and effort spent in validating users’ willingness to pay will be much more useful than maybe engaging in some proof-of-concept to get greater confidence in our development cost.
I hope this post helped show how Monte Carlo simulations could be useful in your product decision-making. Check out this next post, where we’ll roll up our sleeves and show you how to build a Monte Carlo simulation for our hypothetical subscription service.
